Graphs. Application of graphs to problem solving. Constructing graphs based on their characteristics Construct as complete a graph as possible
Null graph and complete graph.
There are some special graphs that appear in many applications of graph theory. For now, we will again consider the graph as a visual diagram illustrating the course of sports competitions. Before the start of the season, while no games have been played yet, there are no edges in the graph. Such a graph consists of only isolated vertices, i.e. of vertices connected by no edges. We will call a graph of this type null graph. In Fig. 3 shows such graphs for cases when the number of commands, or vertices, is 1, 2, 3, 4 and 5. These null graphs are usually denoted by the symbols O1, O2, O3, etc., so On is a null a graph with n vertices and no edges.
Let's consider another extreme case. Let's assume that at the end of the season, each team plays one game against each of the other teams. Then on the corresponding graph each pair of vertices will be connected by an edge. Such a graph is called complete graph. Figure 4 shows complete graphs with the number of vertices n = 1, 2, 3, 4, 5. We denote these complete graphs by U1, U2, U3, U4 and U5, respectively, so that the graph Un consists of 11 vertices and edges, connecting all possible pairs of these vertices. This graph can be thought of as an n-gon in which all the diagonals are drawn.

Having some graph, for example the graph G shown in Fig. 1, we can always turn it into a complete graph with the same vertices by adding the missing edges (that is, edges corresponding to games that are yet to be played). In Fig. 5 we did this for the graph in Fig. 1 (games that have not yet taken place are shown in dotted lines). You can also separately draw a graph corresponding to future games that have not yet been played. For graph G this will result in the graph shown in Fig. 6.
We call this new graph the complement of graph G; It is customary to denote it by G1. Taking the complement of graph G1, we again obtain graph G. The edges of both graphs G1 and G together form a complete graph.
Graphics file format is a way of representing graphical data on external media. Distinguish raster and vector formats graphic files, among which, in turn, there are universal graphic formats And own (original) formats of graphic applications.
Universal graphic formats are “understood” by all applications that work with raster (vector) graphics.
The universal raster graphics format is BMP format. Graphic files in this format have a large information volume, since they allocate 24 bits to store information about the color of each pixel.
In drawings saved in a universal bitmap GIF format, you can only use 256 different colors. This palette is suitable for simple illustrations and pictograms. Graphic files of this format have a small information volume. This is especially important for graphics used in World Wide Web, whose users want the information they requested to appear on the screen as quickly as possible.
Universal raster JPEG format Designed specifically for efficient storage of photographic quality images. Modern computers can reproduce more than 16 million colors, most of which are simply indistinguishable to the human eye. The JPEG format allows you to discard the variety of colors of neighboring pixels that are “excessive” for human perception. Some of the original information is lost, but this ensures a reduction in the information volume (compression) of the graphic file. The user is given the opportunity to determine the degree of file compression. If the image being saved is a photograph that is supposed to be printed on a large-format sheet, then loss of information is undesirable. If this photo is placed on a Web page, then it can be safely compressed tens of times: the remaining information will be enough to reproduce the image on the monitor screen.
Universal vector graphic formats include WMF format, used to store a collection of Microsoft pictures.
Universal EPS format allows you to store information about both raster and vector graphics. It is often used to import files into print production programs.
You will become familiar with your own formats directly in the process of working with graphic applications. They provide the best ratio of image quality and file information volume, but are supported (i.e. recognized and played) only by the application itself that creates the file.
Task 1.
To encode one pixel, 3 bytes are used. The photo, measuring 2048 x 1536 pixels, was saved as an uncompressed file. Determine the size of the resulting file.
Solution:
i = 3 bytes
K= 2048 1536
I — ?
I=Ki
I = 2048 1536 3 = 2 2 10 1.5 2 10 3 = 9 2 20 (bytes) = 9 (MB).
Answer: 9MB.
Task 2.
Uncompressed raster image 128 x 128 pixels takes up 2 KB of memory. What is the maximum possible number of colors in the image palette?
Solution:
K = 128 128
I = 2 KB
N -?
I=Ki
i=I/K
N=2 i
i = (2 1024 8)/(128 128) = (2 2 10 2 3) /(2 7 2 7) = 2 1+10+3 /2 7+7 = 2 14 /2 14 = 1 (bit) .
N = 2 1 = 2.
Answer: 2 colors - black and white.
The most important:
- A graphics file format is a way of representing graphic data on external media. There are raster and vector formats of graphic files, among which, in turn, there are universal graphic formats and proprietary formats of graphic applications.
Theoretical information
Note that in construction problems the solution must be sought among simple undirected graphs (i.e., graphs without multiple edges and without loops). Unfortunately, there is no universal technique that allows you to accurately determine whether a graph with given characteristics can be constructed.
It is important to remember that in any graph the sum of the degrees of all its vertices is an even number, equal to twice the number of edges of the graph, since each edge participates in this sum exactly twice. This result, known to Euler 200 years ago, is often called the handshake lemma. It follows from this that if several people shake hands, then total number The number of handshakes must be even, because two hands are involved in each handshake (each hand is counted as many times as it participated in handshakes). It follows that:
- the number of vertices with odd degrees in any graph is even;
- in any graph with P peaks where P> 2, there are always at least two vertices with the same degrees;
- if in a graph with vertices p> 2 exactly two vertices have the same degree, then in this graph there is always either exactly one vertex of degree 0 or exactly one vertex of degree (P - 1).
When solving problems, you must read the conditions very carefully, since many adjectives that describe the properties of a graph have numerical equivalents. We present a table of such correspondences that are most often found in the formulation of problems (Table 2.9).
After you have obtained all the necessary numbers, you need to try to calculate the missing characteristics of the graph. Sometimes the condition gives the degrees of all or several vertices. In this case, based on the fact that each edge of the graph adds exactly two vertices to its total degree, we can use the formula
X 5 (y /) =2t'
Where T - number of vertices, and the summation is carried out over all vertices from 1 to P.
Tasks
Problem 2.42. Construct a graph on eight vertices that has the following distribution of vertex degrees: two vertices of degree 4; three vertices of degree 3; two vertices of degree 2; one vertex of degree 1.
Solution.
The total degree of all vertices is 2-4 + 3- 3 + 2- 2+1 1=22, which means there are 11 edges in total. It is easier to build graphs based on a vector of degrees, starting from vertices of large degrees. Ver-
Table 2.9
Correspondence between the description of a graph and its properties
|
Adjective |
Numeral |
What does it mean |
|
The graph has exactly one connected component |
||
|
Incoherent |
The graph has more than one component, its diameter is exactly equal to infinity |
|
|
Regular |
5(U;) = SOSHI |
The degrees of all vertices are equal |
|
Regular degree |
з(Уі)=У |
The degrees of all vertices are equal u. If known P(number of vertices), then you can immediately calculate T(number of ribs): y-p? y/2 (P or at must be an even number) |
|
Acyclic |
y= t-p + k = 0 |
The cyclomatic number is zero, the graph has no cycles, it is a tree or a forest (depending on connectivity), such graphs can always be colored in two colors. If two out of three variables are known ( P, t, k), then using the formula you can find the remaining |
|
Tree (or acyclic connected graph) |
y= t- n + 1 =0, whence T- n - 1 |
The cyclomatic number is zero, the graph has no cycles, it is a tree, such graphs can always be colored in two colors. If one of two variables is known ( P or T), then using the formula you can find the second |
|
Bichromatic |
The chromatic number of a graph is two, such graphs can always be colored in two colors, these are bipartite graphs, graphically they are either acyclic graphs or graphs in which all cycles have an even length |
It is better to arrange the buses in the graphical representation of the graph so that as few edges and arcs intersect as possible, and the vertices themselves are grouped according to some similarity criterion. One of the options is shown in Fig. 2.8.
Problem 2.43. Construct a graph on six vertices that has the following distribution of vertex degrees: two vertices of degree 3;
Rice. 2.8.
two vertices of degree 2; one vertex of degree 1; one vertex has an arbitrary degree.
Solution.
The total degree of the vertices is 11, therefore, the remaining vertex must have an odd degree, i.e. 1,3 or 5. Thus, it is possible to construct three different graphs (Fig. 2.9).


Rice. 2.9.
Problem 2.44. Construct a graph with the following vector of vertex degrees: 5 = (1, 2, 2, 3, 4, 4, 5).
Solution.
The total degree is 5 + 8 + 3 + 4+1=21. Since this is an odd number, which contradicts the theorem (the number of edges is half this number, but 21 is not evenly divisible by 2).
Answer. No such graph exists.
Problem 2.45. Construct a graph with the following vector of vertex degrees: 5 = (1, 1,2, 2, 2, 4, 4, 4, 4).
Problem 2.46. Construct a graph with the following vector of vertex degrees: 5 = (5, 5, 6, 6, 6, 6, 6).
Problem 2.47. Construct a graph with the following vector of vertex degrees: 5 = (1, 1, 1,2, 3, 3, 3, 3, 5, 5, 5).
Problem 2.48. Construct a graph with the following vector of vertex degrees: 5 = (3, 3, 3, 3, 3, 3, 3, 7).
Problem 2.49. Construct a graph on six vertices that has the following distribution of vertex degrees: three vertices are of degree 5, and the other three vertices are of unknown degree.
Problem 2.50. Construct a graph on ten vertices, with twice as many edges as vertices, and the following distribution of vertex degrees: two vertices of degree 6; four vertices of degree 5; two vertices of degree 4; two vertices of arbitrary degree - or justify the impossibility of constructing such a graph.
Problem 2.51. Construct a graph on ten vertices that has the following distribution of vertex degrees: one vertex of degree 7; two vertices of degree 6; two vertices of degree 5; two vertices of degree 4; two vertices of degree 3; one vertex of degree 2 - or justify the impossibility of constructing such a graph.
Problem 2.52. Construct a graph on 11 vertices that has the following distribution of vertex degrees: one vertex of degree 7; two vertices of degree 6; two vertices of degree 5; two vertices of degree 4; two vertices of degree 3; one vertex of degree 2 - or justify the impossibility of constructing such a graph.
It is advisable to introduce the concept of a graph after several problems similar to Problem 1 have been analyzed, the decisive consideration in which is graphical representation. It is important that students immediately realize that the same graph can be drawn different ways. In my opinion, there is no need to give a strict definition of a graph, because it is too cumbersome and will only complicate the discussion. At first, an intuitive concept will suffice. When discussing the concept of isomorphism, you can solve several exercises to identify isomorphic and non-isomorphic graphs. One of the central points of the topic is the theorem on the parity of the number of odd vertices. It is important that students fully understand its proof and learn how to apply it to problem solving. When analyzing several problems, I recommend not referring to the theorem, but actually repeating its proof. The concept of graph connectivity is also extremely important. A meaningful consideration here is the consideration of the connectivity component; special attention must be paid to this. Euler graphs are almost a game topic.
First and the main objective The goal that needs to be pursued when studying graphs is to teach schoolchildren to see the graph in the problem statement and to correctly translate the condition into the language of graph theory. You shouldn’t tell both of them to everyone in several classes in a row. It is better to spread classes over 2–3 academic years. (Attached is the development of the lesson “The concept of a graph. Application of graphs to problem solving” in 6th grade).
2. Theoretical material for the topic “Graphs”.
Introduction
Graphs are wonderful mathematical objects; with their help you can solve a lot of different things that are not externally similar friends on each other's tasks. There is a whole section in mathematics - graph theory, which studies graphs, their properties and applications. We will discuss only the most basic concepts, properties of graphs and some ways to solve problems.
Concept of a graph
Let's consider two problems.
Task 1. Space communication has been established between the nine planets of the solar system. Regular rockets fly on the following routes: Earth - Mercury; Pluto - Venus; Earth - Pluto; Pluto - Mercury; Mercury - Vienna; Uranus - Neptune; Neptune - Saturn; Saturn – Jupiter; Jupiter - Mars and Mars - Uranus. Is it possible to fly on regular rockets from Earth to Mars?
Solution: Let's draw a diagram of the condition: we will depict the planets as points, and the rocket routes as lines.
Now it is immediately clear that it is impossible to fly from Earth to Mars.
Task 2. The board has the shape of a double cross, which is obtained by removing the corner squares from a 4x4 square.

Is it possible to bypass it by moving a chess knight and return to the original square, visiting all the squares exactly once?
Solution: Let's number the squares of the board sequentially:
And now, using the figure, we will show that such a traversal of the table, as indicated in the condition, is possible:

We considered two dissimilar problems. However, the solutions to these two problems are united by a common idea - a graphical representation of the solution. At the same time, the pictures drawn for each task turned out to be similar: each picture consists of several dots, some of which are connected by lines.
Such pictures are called graphs. The points are called peaks, and the lines – ribs graph. Note that not every picture of this type will be called a graph. For example. if you are asked to draw a pentagon in your notebook, then such a drawing will not be a graph. We will call a drawing of this type, as in the previous problems, a graph if there is some specific task for which such a drawing was constructed.
Another note concerns the appearance of the graph. Try to check that the graph for the same problem can be drawn in different ways; and vice versa for different tasks you can draw graphs that are identical in appearance. All that matters here is which vertices are connected to each other and which are not. For example, the graph for task 1 can be drawn differently:

Such identical, but differently drawn graphs are called isomorphic.
Degrees of vertices and counting the number of edges of a graph
Let's write down one more definition: The degree of a vertex in a graph is the number of edges emerging from it. In this regard, a vertex with an even degree is called an even vertex, respectively, a vertex with an odd degree is called an odd vertex.
One of the main theorems of graph theory is related to the concept of vertex degree - the theorem on the fairness of the number of odd vertices. We will prove it a little later, but first, for illustration, we will consider the problem.
Task 3. There are 15 telephones in the town of Malenky. Is it possible to connect them with wires so that each phone is connected to exactly five others?
Solution: Let's assume that such a connection between telephones is possible. Then imagine a graph in which the vertices represent telephones, and the edges represent the wires connecting them. Let's count how many wires there are in total. Each phone has exactly 5 wires connected, i.e. the degree of each vertex of our graph is 5. To find the number of wires, you need to sum up the degrees of all the vertices of the graph and divide the resulting result by 2 (since each wire has two ends, then when summing the degrees, each wire will be taken 2 times). But then the number of wires will be different. But this number is not an integer. This means that our assumption that each phone can be connected to exactly five others turned out to be incorrect.
Answer. It is impossible to connect phones this way.
Theorem: Any graph contains an even number of odd vertices.
Proof: The number of edges of a graph is equal to half the sum of the degrees of its vertices. Since the number of edges must be an integer, the sum of the degrees of the vertices must be even. And this is only possible if the graph contains an even number of odd vertices.
Graph connectivity
There is another important concept related to graphs - the concept of connectivity.
The graph is called coherent, if any two of its vertices can be connected by, those. continuous sequence of edges. There are a number of problems whose solution is based on the concept of graph connectivity.
Task 4. There are 15 cities in the country of Seven, each city is connected by roads to at least seven others. Prove that it is fashionable to get from every city to any other.
Proof: Consider two arbitrary cities A and B and assume that there is no path between them. Each of them is connected by roads to at least seven others, and there is no city that is connected to both cities in question (otherwise there would be a path from A to B). Let's draw a part of the graph corresponding to these cities:

Now it is clearly visible that we have received at least 16 different cities, which contradicts the conditions of the problem. This means the statement has been proven by contradiction.
If we take into account the previous definition, then the statement of the problem can be reformulated in another way: “Prove that the road graph of the country Seven is connected.”
Now you know what a connected graph looks like. A disconnected graph has the form of several “pieces”, each of which is either a separate vertex without edges or a connected graph. You can see an example of a disconnected graph in the figure:

Each such individual piece is called connected component of the graph. Each connected component represents a connected graph and all the statements that we have proven for connected graphs hold for it. Let's look at an example of a problem that uses a connected component:
Problem 5. In the Far Far Away Kingdom there is only one type of transport - a flying carpet. There are 21 carpet lines leaving the capital, one from the city of Dalniy, and 20 from all other cities. Prove that you can fly from the capital to the city of Dalniy.
Proof: It is clear that if you draw a graph of the carpet of the Kingdom, it may be incoherent. Let's look at the connectivity component that includes the Kingdom capital. There are 21 carpets coming out of the capital, and 20 from any other city except the city of Dalniy, therefore, in order for the law on an even number of odd vertices to be fulfilled, it is necessary that the city of Dalniy be included in the same component of connectivity. And since the connected component is a connected graph, then from the capital there is a path along the carpets to the city of Dalniy, which was what needed to be proven.
Euler graphs
You've probably encountered tasks in which you need to draw a shape without lifting your pencil from the paper and drawing each line only once. It turns out that such a problem is not always solvable, i.e. There are figures that cannot be drawn using this method. The question of the solvability of such problems is also included in graph theory. It was first explored in 1736 by the great German mathematician Leonhard Euler, solving the problem of the Königsberg bridges. Therefore, graphs that can be drawn in this way are called Euler graphs.
Task 6. Is it possible to draw the graph shown in the figure without lifting the pencil from the paper and drawing each edge exactly once?

Solution. If we draw the graph as stated in the condition, then we will enter each vertex, except the initial and final ones, the same number of times as we exit it. That is, all vertices of the graph, except two, must be even. Our graph has three odd vertices, so it cannot be drawn in the way specified in the condition.
Now we have proven the theorem about Euler graphs:
Theorem: An Euler graph must have at most two odd vertices.
And in conclusion - the problem of the Königsberg bridges.
Task 7. The figure shows a diagram of bridges in the city of Königsberg.
Is it possible to take a walk so that you cross each bridge exactly once?

3. Problems for the topic “Graphs”
The concept of a graph.
1. On a 3x3 square board, 4 knights are placed as shown in Fig. 1. Is it possible, after making several moves with the knights, to rearrange them to the position shown in Fig. 2?
Rice. 1 |
Rice. 2 |
Solution. Let's number the squares of the board as shown in the figure:
Let us assign a point on the plane to each cell and, if one can get from one cell to another by moving a chess knight, then we will connect the corresponding points with a line. The initial and required placement of the knights are shown in the figures:
 |
 |
For any sequence of knight moves, their order obviously cannot change. Therefore, it is impossible to rearrange the horses in the required manner.
2. In the country of Digit there are 9 cities with names 1, 2, 3, 4, 5, 6, 7, 8, 9. A traveler discovered that two cities are connected by an airline if and only if the two-digit number formed by the names cities, divided by 3. Is it possible to fly by air from city 1 to city 9?
Solution. By assigning a dot to each city and connecting the dots with a line, if the sum of the numbers is divisible by 3, we get a graph in which the numbers 3, 5, 9 are connected to each other, but not connected to the rest. This means that you cannot fly from city 1 to city 9.
Degrees of vertices and counting the number of edges.
3. There are 100 cities in a state, and each city has 4 roads. How many roads are there in the state?
Solution. Let's count the total number of roads leaving the city - 100 . 4 = 400. However, with this calculation, each road is counted 2 times - it leaves one city and enters another. This means that there are two times fewer roads in total, i.e. 200.
4. There are 30 people in the class. Could it be that 9 people have 3 friends, 11 have 4 friends, and 10 have 5 friends?
Answer. No (theorem on the parity of the number of odd vertices).
5. The king has 19 vassals. Could it be that each vassal has 1, 5 or 9 neighbors?
Answer. No, he can not.
6. Can a state in which exactly 3 roads exit from each city have exactly 100 roads?
Solution. Let's count the number of cities. The number of roads is equal to the number of cities x multiplied by 3 (the number of roads leaving each city) and divided by 2 (see problem 3). Then 100 = 3x/2 => 3x = 200, which cannot happen with natural x. This means there cannot be 100 roads in such a state.
7. Prove that the number of people who have ever lived on Earth and made an odd number of handshakes is even.
The proof follows directly from the theorem on the parity of the number of odd vertices in a graph.
Connectivity.
8. In the country, 100 roads leave each city and from each city you can get to any other. One road was closed for repairs. Prove that now you can get from any city to any other.
Proof. Let's consider the connectivity component, which includes one of the cities, the road between which was closed. By the theorem on the parity of the number of odd vertices, it also includes the second city. This means you can still find a route and get from one of these cities to another.
Euler graphs.
9. There is a group of islands connected by bridges so that from each island you can get to any other. The tourist walked around all the islands, crossing each bridge once. He visited Threefold Island three times. How many bridges lead from Troyekratnoye if a tourist
a) didn’t start with it and didn’t end with it?
b) started with it, but didn’t finish with it?
c) started with it and ended with it?
10. The picture shows a park divided into several parts by fences. Is it possible to walk through the park and its surroundings so that you can climb over each fence once?

1736, Koenigsberg. The Pregelya River flows through the city. There are seven bridges in the city, located as shown in the figure above. Since ancient times, the residents of Königsberg have struggled with a riddle: is it possible to cross all the bridges, walking on each one only once? This problem was solved both theoretically, on paper, and in practice, on walks - passing along these very bridges. No one was able to prove that this was impossible, but no one could make such a “mysterious” walk across the bridges.
The famous mathematician Leonhard Euler managed to solve the problem. Moreover, he solved not only this specific problem, but came up with a general method for solving similar problems. When solving the problem of the Königsberg bridges, Euler proceeded as follows: he “compressed” the land into points, and “stretched” the bridges into lines. Such a figure, consisting of points and lines connecting these points, is called COUNT.
A graph is a collection of a non-empty set of vertices and connections between vertices. Circles are called vertices of the graph, lines with arrows are arcs, and lines without arrows are edges.
Types of graphs:
1. Directed graph(briefly digraph) - whose edges are assigned a direction.
2. Undirected graph is a graph in which there is no direction of lines.
3. Weighted graph– arcs or edges have weight (additional information).



Solving problems using graphs:
Task 1.

Solution: Let us denote the scientists as the vertices of the graph and draw lines from each vertex to four other vertices. We get 10 lines, which will be considered handshakes.
Task 2.
There are 8 trees growing on the school site: apple tree, poplar, birch, rowan, oak, maple, larch and pine. Rowan is higher than larch, apple tree is higher than maple, oak is lower than birch, but higher than pine, pine is higher than rowan, birch is lower than poplar, and larch is higher than apple tree. Arrange the trees from shortest to tallest.
Solution:
The vertices of the graph are trees, indicated by the first letter of the tree name. There are two relationships in this task: “to be lower” and “to be higher.” Consider the relation “to be lower” and draw arrows from a lower tree to a higher one. If the problem says that the mountain ash is taller than the larch, then we put an arrow from the larch to the mountain ash, etc. We get a graph that shows that the shortest tree is maple, followed by apple, larch, rowan, pine, oak, birch and poplar.

Task 3.
Natasha has 2 envelopes: regular and air, and 3 stamps: rectangular, square and triangular. In how many ways can Natasha choose an envelope and a stamp to send a letter?
Solution:

Below is a breakdown of the tasks.


 Order 343 mail. Order by Russian post. Consequences of failure to appear in court when summoned
Order 343 mail. Order by Russian post. Consequences of failure to appear in court when summoned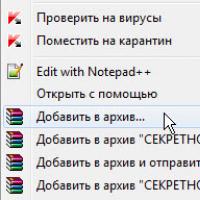 How to put a password on a folder on a Windows computer without and with programs
How to put a password on a folder on a Windows computer without and with programs Pluton – Free Bootstrap HTML5 One Page Template
Pluton – Free Bootstrap HTML5 One Page Template History of ZX Spectrum: Myths and reality New Spectrum
History of ZX Spectrum: Myths and reality New Spectrum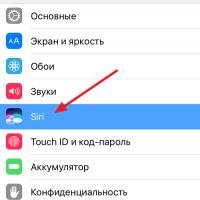 Voice assistant Siri from Apple Siri functions on iPhone 6s
Voice assistant Siri from Apple Siri functions on iPhone 6s How to roll back to a previous version of iOS?
How to roll back to a previous version of iOS?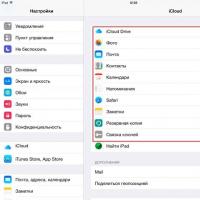 Unlock iPad in four days
Unlock iPad in four days